If p = 1! + (2x2!) + (3x3!) + (4x4!)...... + (10x10!), what is the remainder when p+2 is divided by 11!? Answer: 1 Explanation: p = 1! + (2x2!) + (3x3!) + (4x4!)...... + (10x10!) p = (1x1!) + (2x2!) + (3x3!) + (4x4!)...... + (10x10!) But, (1x1!) = 2! – 1! (2x2!) = 3! – 2! (3x3!) = 4! – 3! And so on. Hence, p = 2! – 1! + 3! – 2! + 4! – 3! + 5! – 4! + 6! – 5! + 7! – 6! … [Read more...] about Number Properties – Factorial & Remainders
GRE Problem Solving
Statistics – Mean, Median, Range
The maximum mark in an examination is 100 and the minimum is 0. The average mark of seven students such that no two of them have scored the same marks is 88. If the median score is 92 and all the marks are integers, what is the maximum possible difference between the largest and the smallest mark obtained by these seven students? Answer: 54 Explanation: Average mark of … [Read more...] about Statistics – Mean, Median, Range
Geometry Triangle – Equating Areas
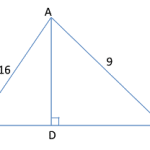
In a triangle ABC, AB = 16, AC = 9. Find the length of the altitude to BC if the circumradius is 9. Answer: 8 Explanation: Consider the figure below. We know that, Area of a triangle = abc/4R where a,b,c are the sides of the triangle and R is the circumradius. Hence, (AB x BC x AC)/4R = (1/2) x BC x AD (16 x BC x 9)/36 = (1/2) x BC x AD Therefore, AD = 8. … [Read more...] about Geometry Triangle – Equating Areas
Algbera Practice: Functions
A function is defined as f(x+2) = 3 + f(x) when x is even f(x+2) = x + f(x) when x is odd f(1) = 4 and f(2) = 3 Find f(f(f(1))) + f(f(f(2))) Answer: 17 Explanation: f(f(f(1))) + f(f(f(2))) = f(f(4)) + f(f(3)) Now f(4) can be found by using the definition of the function when x is even. Take x = 2. f(2+2) = 3 + f(2) f(4) = 3 + 3 f(4) = 6 Likewise, f(3) can be … [Read more...] about Algbera Practice: Functions
Arithmetic and Geometric Progressions
The second, the first and the third term of an A.P whose common difference is non zero form a G.P in that order. Find its common ratio. Answer: -2 Explanation: Let the terms in GP be a, ar, ar2. Hence the terms ar, a and ar2 are in AP. Therefore, a – ar = ar2– a ‘a’ cannot be 0. Hence, 1 – r = r2 – 1 r2 + r -2 = 0 (r + 2)(r – 1) = 0 Now r cannot be ‘1’ … [Read more...] about Arithmetic and Geometric Progressions